Демографический анализ:
как построить таблицу смертности
| ЦН ЭФ МГУ | Описательная статистика | Демографический анализ | Демографические прогнозы | |
| Начало | История демографии | История мирового населения | Демография для начинающих |
Из курсов Александра Александровича Авдеева, читавшихся в Страсбургском университете в 2003-2005 годах и в 2007-2025 годах в Институте демографии Парижского университета Пантеон-Сорбонна (IDUP)
(перевод на русский и адаптация к традиции русской терминологии еще не закончены)
|
|
Демографический анализ: |
|
||||||||||
|
|
|
|
Что такое таблица смертности Определение: Таблица смертности - это математическая модель, которая выдает вероятности выжить (или нет) в течение определенного периода времени для индивидуума, достигшего некоторого заданного возраста. Принципы построения таблиц смертности были разработаны еще в 18-19 веках, а алгоритм расчетов был окончательно усовершенствован в середине прошлого века. Обобщение: Построение таблицы смертности представляет собой один вариантов (методов) статистического анализа надежности на основе данных типа времени жизни. Для чего нужны таблицы смертности: Таблицы смертности служит, прежде всего, для того, чтобы ответить на вопрос, как долго пробудет в некотором состоянии индивид (например, в состоянии "живой"), обладающий определенными характеристиками (например, пол и точный возраст)? Нетрудно увидеть, что ответ на этот вопрос крайне важен, например, для страховых компаний, которые устанавливают размеры ежегодных взносов на основе ожидаемой длительность их выплаты. Уточнение и оговорки: Исторически в русском и французском языках термин "таблица смертности" (table de mortalité) часто используется как родовое название любых демографических таблиц, представляющих длительности различных состояний. В английском языке употребляется термины "life table" - таблица жизни и "survival analysis" анализ выживания. Хотя, на самом деле, принципы построения таблиц смертности применяются к анализу длительности любых состояний, например, строятся таблицы вступления в брак холостяков, или таблицы рождаемости для бездетных и т.д. Уходя от демографии в чистом виде, можно также подумать об оценке длительности работы агрегата, например автомобиля или компьютера, до первой поломки. В данной инструкции мы будем говорить о собственно таблице смертности, которая моделирует длительность жизни от рождения до смерти. Инструкция представляет один простейших из алгоритмов расчета таблицы смертности (который иногда несправедливо назвают "актуарным"), и все серьезные вопросы теории и методологии оставлены за скобками. Исходные данные или борьба за качество: Исходными данными для построения таблиц смертности являются числа живущих и умерших в определенном возрасте. Эти данные являются экзогенными переменными модели и должны быть приведены к определенному периоду, как правило одному году. Главной эндогенной переменной модели является вероятность выживания от одного до другого точного возраста. Качество исходных данных определяет точность таблиц смертности. |
Вечный вопрос российской жизни: "Кому достается
национальных доход?"
О пророческой силе
советского искусства и фольклора |
|
|
Наука
|
Как построить таблицу
смертности: Сначала введем обозначения, которые затем будут использоваться в формулах (заметим, что это не наше изобретение и эти символы используются для обозначения элементов таблиц смертности во всех странах и на всех языках): nDx – число умерших в возрасте [x, x+n) / то есть в возрастном интервале от х-ого до (x+n) – ого дня рождения / в данном году;
n –
может быть равным 1 для всех возрастов, кроме последнего
(полная одногодичная возрастная структура) или 4 для возраста
1-4 года, или 5 – для пятилетних групп, или
10 и т.д. Nota : в нашем случае все данные приведены к году, но, в принципе, можно использовать и данные за несколько смежных лет. nPx – среднегодовая численность населения в возрасте [x, x+n), еще называется средним населением, или население на середину года (интервала времени). Nota: Обычно, таблицы смертности строятся всегда для периода длительностью 1 год. То есть они представляют модель смертности в течение одного календарного года. nMx – наблюдаемый коэффициент смертности среднегодовая численность населения в возрасте [x, x+n), еще называется средним населением, или население на середину года.
Nota: если данные относятся к периоду длиннее одного года, например, если интервал времени к которому относятся исходные данные равен 6 годам, то тогда знаменатель в формуле (1) надо будет умножить на 6 (по этому поводу см. инструкции по расчету общих и частных коэффициентов движения населения) Если предположить (основная гипотеза), что наблюдаемый коэффициент смертности является более или менее точной оценкой средней силы смертности в интервале возраста, то можно рассчитать вероятность умереть в течение этого интервала. Эта вероятность очевидно зависит от величины силы смертности и длительности интервала. Другими словами, чем длиннее интервал, тем больше вероятность умереть, хотя плотность распределения этой вероятности (сила смертности) внутри интервала, то есть в каждый миг, может быть и постоянной... Часто говорят о "моментальной силе смертности" (memento more, что в переводе с античного означает и т.д. по Гайдаю) Обозначим эту вероятность как nqx– вероятность умереть в возрасте [x, x+n), которая можно расчитать по формуле "актуариев", вывод которой пока оставим за скобками:
\({}_n q _x = \frac{n \cdot {}_n m _x}{1 + (n - {}_n a_x) {}_n m_x}\) (2) где nmx – оценка средней силы смертности в [x, x+n), по поводу которой было решено, что она примерно равна nMx nax– средняя длительность жизни в возрасте [x, x+n), для тех, кто умер в этом интервале (средняя длительность жизни в последнем интервале возраста). Поскольку в статистике смертности эта информация отсутствует, то обычно предполагается, что они прожили ровно половину этого интервала. Это предположение очень неправильно для возраста 0 лет, для старших возрастов, и уж особенно неприятно, если приходится работать с интервалами возраста превышающими 1 год, но ничего не поделаешь, потом можно будет сделать уточнения.
Итак считаем, что \({}_n a _x = \frac{n}{2} = 0.5 \cdot n \ \) (3) В принципе, теперь формулу (2) можно было бы упростить, переписав, следующим образом: \({}_n q_x=\frac{2\cdot n\cdot {}_n m_x}{2+n\cdot {}_n m_x}\), что обычно и делают демографы, но за пределами учебного класса лучше не пользоваться упрощенной формулой, а постараться оценить параметр nax , входящий в соотношение (2) Можно также считать вероятность умереть исходя из гипотезы, что сила смертности в любой точке интервала между x и x+n является постоянной и приблизительно равна коэффициенту смертности nmx, в этом случае число живущих будет изменяться (в нашем случае - уменьшаться) по экспоненте, а верятность умереть будет описываться экспоненциальной функцией с параметрами n и nmx вот так: \({}_n q _x = 1 - e^{- n \cdot {}_n m _x}\) (4) Поскольку сегодня компьютер облегчает и ускоряет все расчеты, то лучше, конечно, использовать формулу (4). Теперь считаем nqx для всех интервалов, исключая последний, для которого она, естественно, равна 1. Теперь можно строить таблицу смертности, которая есть не что иное, как табулированная функция вероятности дожить от рождения до точного возраста х. Она обычно обозначается как lx в англоязычной и демографической литературе и Sx – во франкоязычной литературе и статистическом анализе данных типа времени жизни (survival analysis). Учитывая некоторые наши географические особенности, остановимся на втором варианте. Sx – вероятность дожить от рождения до точного возраста x Поскольку вероятности очень малы, их умножают на 100 000 (или на 10 000) и называют этот множитель корнем таблицы. Его может выбирать автор в зависимости от повозрастных уровней смертности: чем ниже уровень, тем больше корень таблицы. Таким образом, для современных таблиц смертности лучше выбирать S0 = 100 000, и \(S_{x + 1} = S_x (1 - {}_n q_x)\) \(S_{x + 2} = S_{x + 1} (1 - {}_n q_{x + 1})\)=\(S_x (1 - {}_n q_x)\)(\(1 - {}_n q_{x + 1})\), и т.д. (5) Следующим элементом таблицы смертности является число лет, или число человеко-лет, прожитых в интервале возраста [x, x+n). Оно обозначается как nLx. Его еще называют числом живущих. nLx – число лет, прожитых населением в интервале возраста от х до х+n. Очевидно, что тот, кто не умер в этом интервале прожил ровно n лет, а поскольку нам уже известно, что до конца интервала дожило Sx+1 человек, а умерло ndx ndx=Sx – Sx+n (6) которые прожили в соответствии с нашей гипотезой (3) ровно половину n. Таким образом, для всех групп, кроме последней, можно рассчитать nLx, как \({}_n L_x = \frac{S_x + S_{x + 1}}{2} \cdot n \ \) (7) или \({}_n L_x = S_{x + 1} \cdot n + {}_n d_x \cdot {}_n a_x \ \) если же, гипотеза о том, что те, кто умер в течение интервала от x до x+n, прожили в среднем его половину, кажется слишком неправдоподобной, тогда нужно считать, что \({}_n L_x = S_{x + 1} \cdot n + {}_n d_x \cdot {}_n a_x \ \) (7bis) Для последней (ω) возрастной группы рассчитаем nLx , как \({}_{\infty} L_{\omega} = \frac{{S_{\omega}} }{{}_{\infty} m_x} = \frac{{}_{\infty} {d_{\omega}} }{{}_{\infty} m_x}\ \) (8) где ∞Sω число доживших до последнего определенного возраста в таблице смертности и ∞mω = ∞Mω наблюдаемый коэффициент смертности в последней возрастной группе.
Наконец, последний важный элемент таблицы смертности – средняя продолжительность предстоящей жизни, для тех, кто дожил до определенного возраста х, обозначаемая обычно (ех). и представляющая собой не что иное, как средний возраст умерших для доживших до возраста х. Этот показатель можно рассчитывать на основе чисел доживающих (Sx), чисел живущих (nLx) или же чисел умерших в каждом интервале возраста (ndx). Наиболее корректен расчет на основе числе живущих (при условии правильной оценки средней длительности жизни в последнем интервале возраста nax): \(e_x = \frac{\underset{y = x}{\overset{\omega}{\sum}} {}_n L_y}{S_x}\) (9) Обычно сумму nLx рассчитывают в отдельной колонке. Наиболее популярный является средняя продолжительность жизни новорожденных е0. Картинки получаются красивые. 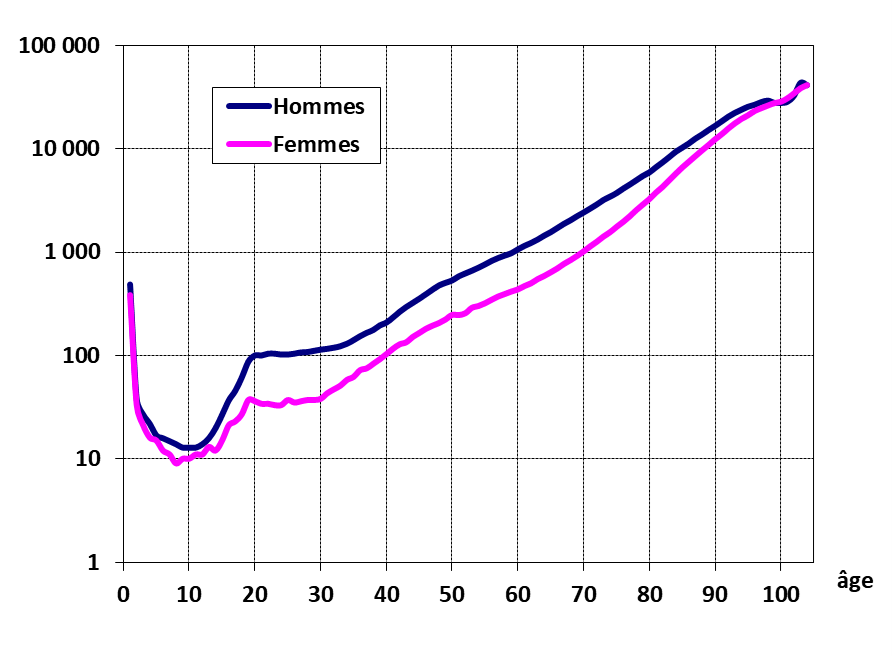Вот например Вероятность умереть (nqx) во Франции в 2001-2002 году
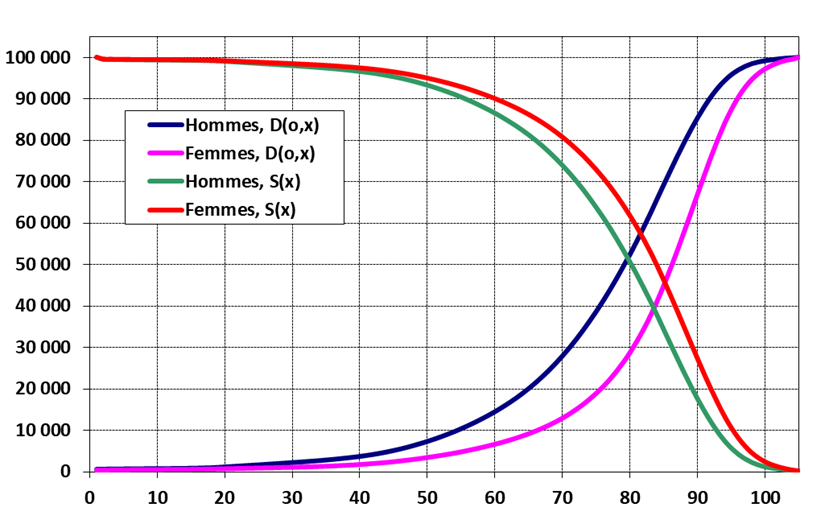
Вероятность дожития (Sx) и смерти (100 000 – Sx) во Франции в 2001-2002 году
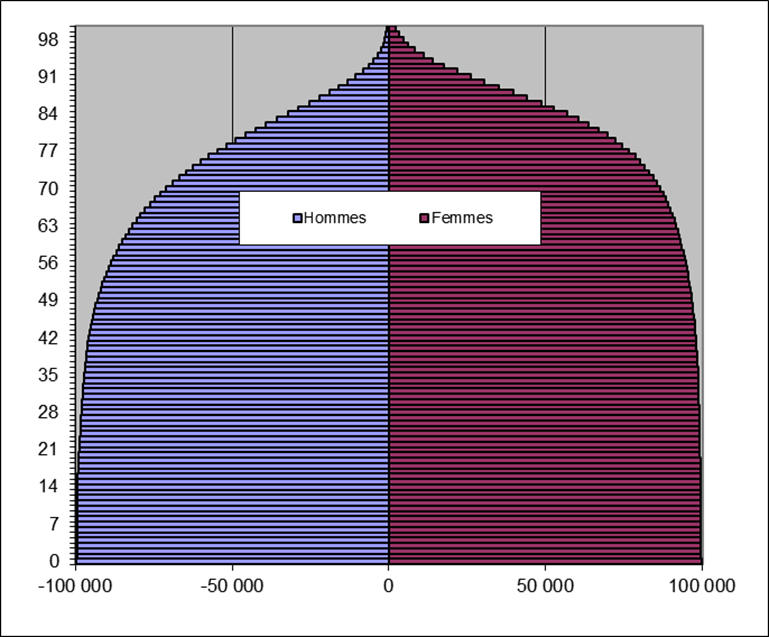
Числа умирающих (Sx – Sx+1) во Франции в 2001-2002 году
Стационарное население (nLx)
соответствующее таблице смертности
|
|
Наука............................