Site d'Alexandre Avdeev pour les étudiants en démographie
La distribution F de Fisher

[Ennoncé théorique] [Distribution F pour p = 5%] [Distribution F pour p = 1%]
![]()
 |
Site d'Alexandre Avdeev pour les étudiants en démographie La distribution F de Fisher |
 |
|
[Ennoncé théorique] [Distribution F pour p = 5%] [Distribution F pour p = 1%]
|
||
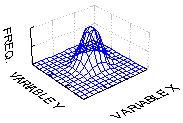
La forme de la distribution F de Fisher pour chaque niveau de signification dépend des degrés de liberté pour le numérateur (df1) et de degrés de liberté pour le dénominateur (df1). La graphique à gauche montre le changement de la probablilité (p) en fonction du score d'un rapporte avec 10 degrés de liberté pour le numérateur et pour le dénominateur.
La fonction de la densité de F- distribution de Fisher (pour x > 0 et
pour ![]() = 1, 2, ...;
= 1, 2, ...;
![]() = 1, 2, ...) est suivante:
= 1, 2, ...) est suivante:
| f(x) = { |
| x( |
0 ![]() x <
x <
![]()
![]() = 1, 2, ...,
= 1, 2, ..., ![]() = 1, 2, ...
= 1, 2, ...
où ![]() ,
, ![]() - degrés de
liberté et
- degrés de
liberté et ![]() - fonction
gamma
- fonction
gamma
|
DL pour le numérateur (df1) |
|||||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
20 |
25 |
30 |
40 |
||
|
DL pour le dénominateur (df2) |
1 |
161.4 |
199.5 |
215.7 |
224.6 |
230.2 |
234.0 |
236.8 |
238.9 |
240.5 |
241.9 |
248.0 |
249.3 |
250.1 |
251.1 |
|
2 |
18.5 |
19.0 |
19.2 |
19.2 |
19.3 |
19.3 |
19.4 |
19.4 |
19.4 |
19.4 |
19.4 |
19.5 |
19.5 |
19.5 |
|
|
3 |
10.1 |
9.6 |
9.3 |
9.1 |
9.0 |
8.9 |
8.9 |
8.8 |
8.8 |
8.8 |
8.7 |
8.6 |
8.6 |
8.6 |
|
|
4 |
7.7 |
6.9 |
6.6 |
6.4 |
6.3 |
6.2 |
6.1 |
6.0 |
6.0 |
6.0 |
5.8 |
5.8 |
5.7 |
5.7 |
|
|
5 |
6.6 |
5.8 |
5.4 |
5.2 |
5.1 |
5.0 |
4.9 |
4.8 |
4.8 |
4.7 |
4.6 |
4.5 |
4.5 |
4.5 |
|
|
6 |
6.0 |
5.1 |
4.8 |
4.5 |
4.4 |
4.3 |
4.2 |
4.1 |
4.1 |
4.1 |
3.9 |
3.8 |
3.8 |
3.8 |
|
|
7 |
5.6 |
4.7 |
4.3 |
4.1 |
4.0 |
3.9 |
3.8 |
3.7 |
3.7 |
3.6 |
3.4 |
3.4 |
3.4 |
3.3 |
|
|
8 |
5.3 |
4.5 |
4.1 |
3.8 |
3.7 |
3.6 |
3.5 |
3.4 |
3.4 |
3.3 |
3.2 |
3.1 |
3.1 |
3.0 |
|
|
9 |
5.1 |
4.3 |
3.9 |
3.6 |
3.5 |
3.4 |
3.3 |
3.2 |
3.2 |
3.1 |
2.9 |
2.9 |
2.9 |
2.8 |
|
|
10 |
5.0 |
4.1 |
3.7 |
3.5 |
3.3 |
3.2 |
3.1 |
3.1 |
3.0 |
3.0 |
2.8 |
2.7 |
2.7 |
2.7 |
|
|
11 |
4.8 |
4.0 |
3.6 |
3.4 |
3.2 |
3.1 |
3.0 |
2.9 |
2.9 |
2.9 |
2.6 |
2.6 |
2.6 |
2.5 |
|
|
12 |
4.7 |
3.9 |
3.5 |
3.3 |
3.1 |
3.0 |
2.9 |
2.8 |
2.8 |
2.8 |
2.5 |
2.5 |
2.5 |
2.4 |
|
|
13 |
4.7 |
3.8 |
3.4 |
3.2 |
3.0 |
2.9 |
2.8 |
2.8 |
2.7 |
2.7 |
2.5 |
2.4 |
2.4 |
2.3 |
|
|
14 |
4.6 |
3.7 |
3.3 |
3.1 |
3.0 |
2.8 |
2.8 |
2.7 |
2.6 |
2.6 |
2.4 |
2.3 |
2.3 |
2.3 |
|
|
15 |
4.5 |
3.7 |
3.3 |
3.1 |
2.9 |
2.8 |
2.7 |
2.6 |
2.6 |
2.5 |
2.3 |
2.3 |
2.2 |
2.2 |
|
|
16 |
4.5 |
3.6 |
3.2 |
3.0 |
2.9 |
2.7 |
2.7 |
2.6 |
2.5 |
2.5 |
2.3 |
2.2 |
2.2 |
2.2 |
|
|
17 |
4.5 |
3.6 |
3.2 |
3.0 |
2.8 |
2.7 |
2.6 |
2.5 |
2.5 |
2.4 |
2.2 |
2.2 |
2.1 |
2.1 |
|
|
18 |
4.4 |
3.6 |
3.2 |
2.9 |
2.8 |
2.7 |
2.6 |
2.5 |
2.5 |
2.4 |
2.2 |
2.1 |
2.1 |
2.1 |
|
|
19 |
4.4 |
3.5 |
3.1 |
2.9 |
2.7 |
2.6 |
2.5 |
2.5 |
2.4 |
2.4 |
2.2 |
2.1 |
2.1 |
2.0 |
|
|
20 |
4.4 |
3.5 |
3.1 |
2.9 |
2.7 |
2.6 |
2.5 |
2.4 |
2.4 |
2.3 |
2.1 |
2.1 |
2.0 |
2.0 |
|
|
21 |
4.3 |
3.5 |
3.1 |
2.8 |
2.7 |
2.6 |
2.5 |
2.4 |
2.4 |
2.3 |
2.1 |
2.0 |
2.0 |
2.0 |
|
|
22 |
4.3 |
3.4 |
3.0 |
2.8 |
2.7 |
2.5 |
2.5 |
2.4 |
2.3 |
2.3 |
2.1 |
2.0 |
2.0 |
1.9 |
|
|
23 |
4.3 |
3.4 |
3.0 |
2.8 |
2.6 |
2.5 |
2.4 |
2.4 |
2.3 |
2.3 |
2.0 |
2.0 |
2.0 |
1.9 |
|
|
24 |
4.3 |
3.4 |
3.0 |
2.8 |
2.6 |
2.5 |
2.4 |
2.4 |
2.3 |
2.3 |
2.0 |
2.0 |
1.9 |
1.9 |
|
|
25 |
4.2 |
3.4 |
3.0 |
2.8 |
2.6 |
2.5 |
2.4 |
2.3 |
2.3 |
2.2 |
2.0 |
2.0 |
1.9 |
1.9 |
|
|
26 |
4.2 |
3.4 |
3.0 |
2.7 |
2.6 |
2.5 |
2.4 |
2.3 |
2.3 |
2.2 |
2.0 |
1.9 |
1.9 |
1.9 |
|
|
27 |
4.2 |
3.4 |
3.0 |
2.7 |
2.6 |
2.5 |
2.4 |
2.3 |
2.3 |
2.2 |
2.0 |
1.9 |
1.9 |
1.8 |
|
|
28 |
4.2 |
3.3 |
2.9 |
2.7 |
2.6 |
2.4 |
2.4 |
2.3 |
2.2 |
2.2 |
2.0 |
1.9 |
1.9 |
1.8 |
|
|
29 |
4.2 |
3.3 |
2.9 |
2.7 |
2.5 |
2.4 |
2.3 |
2.3 |
2.2 |
2.2 |
1.9 |
1.9 |
1.9 |
1.8 |
|
|
30 |
4.2 |
3.3 |
2.9 |
2.7 |
2.5 |
2.4 |
2.3 |
2.3 |
2.2 |
2.2 |
1.9 |
1.9 |
1.8 |
1.8 |
|
|
40 |
4.1 |
3.2 |
2.8 |
2.6 |
2.4 |
2.3 |
2.2 |
2.2 |
2.1 |
2.1 |
1.8 |
1.8 |
1.7 |
1.7 |
|
|
50 |
4.0 |
3.2 |
2.8 |
2.6 |
2.4 |
2.3 |
2.2 |
2.1 |
2.1 |
2.0 |
1.8 |
1.7 |
1.7 |
1.6 |
|
|
60 |
4.0 |
3.2 |
2.8 |
2.5 |
2.4 |
2.3 |
2.2 |
2.1 |
2.0 |
2.0 |
1.7 |
1.7 |
1.6 |
1.6 |
|
|
120 |
3.9 |
3.1 |
2.7 |
2.4 |
2.3 |
2.2 |
2.1 |
2.0 |
2.0 |
1.9 |
1.7 |
1.6 |
1.6 |
1.5 |
|
|
200 |
3.9 |
3.0 |
2.6 |
2.4 |
2.3 |
2.1 |
2.1 |
2.0 |
1.9 |
1.9 |
1.6 |
1.6 |
1.5 |
1.5 |
|
|
500 |
3.9 |
3.0 |
2.6 |
2.4 |
2.2 |
2.1 |
2.0 |
2.0 |
1.9 |
1.8 |
1.6 |
1.5 |
1.5 |
1.4 |
|
|
1000 |
3.9 |
3.0 |
2.6 |
2.4 |
2.2 |
2.1 |
2.0 |
1.9 |
1.9 |
1.8 |
1.6 |
1.5 |
1.5 |
1.4 |
|
|
DL pour le numérateur |
|||||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
20 |
25 |
30 |
40 |
||
|
DL pour le dénominateur |
1 |
4052.2 |
4999.3 |
5403.5 |
5624.3 |
5764.0 |
5859.0 |
5928.3 |
5981.0 |
6022.4 |
6055.9 |
6208.7 |
6239.9 |
6260.4 |
6286.4 |
|
2 |
98.5 |
99.0 |
99.2 |
99.3 |
99.3 |
99.3 |
99.4 |
99.4 |
99.4 |
99.4 |
99.4 |
99.5 |
99.5 |
99.5 |
|
|
3 |
34.1 |
30.8 |
29.5 |
28.7 |
28.2 |
27.9 |
27.7 |
27.5 |
27.3 |
27.2 |
26.7 |
26.6 |
26.5 |
26.4 |
|
|
4 |
21.2 |
18.0 |
16.7 |
16.0 |
15.5 |
15.2 |
15.0 |
14.8 |
14.7 |
14.5 |
14.0 |
13.9 |
13.8 |
13.7 |
|
|
5 |
16.3 |
13.3 |
12.1 |
11.4 |
11.0 |
10.7 |
10.5 |
10.3 |
10.2 |
10.1 |
9.6 |
9.4 |
9.4 |
9.3 |
|
|
6 |
13.7 |
10.9 |
9.8 |
9.1 |
8.7 |
8.5 |
8.3 |
8.1 |
8.0 |
7.9 |
7.4 |
7.3 |
7.2 |
7.1 |
|
|
7 |
12.2 |
9.5 |
8.5 |
7.8 |
7.5 |
7.2 |
7.0 |
6.8 |
6.7 |
6.6 |
6.2 |
6.1 |
6.0 |
5.9 |
|
|
8 |
11.3 |
8.6 |
7.6 |
7.0 |
6.6 |
6.4 |
6.2 |
6.0 |
5.9 |
5.8 |
5.4 |
5.3 |
5.2 |
5.1 |
|
|
9 |
10.6 |
8.0 |
7.0 |
6.4 |
6.1 |
5.8 |
5.6 |
5.5 |
5.4 |
5.3 |
4.8 |
4.7 |
4.6 |
4.6 |
|
|
10 |
10.0 |
7.6 |
6.6 |
6.0 |
5.6 |
5.4 |
5.2 |
5.1 |
4.9 |
4.8 |
4.4 |
4.3 |
4.2 |
4.2 |
|
|
11 |
9.6 |
7.2 |
6.2 |
5.7 |
5.3 |
5.1 |
4.9 |
4.7 |
4.6 |
4.5 |
4.1 |
4.0 |
3.9 |
3.9 |
|
|
12 |
9.3 |
6.9 |
6.0 |
5.4 |
5.1 |
4.8 |
4.6 |
4.5 |
4.4 |
4.3 |
3.9 |
3.8 |
3.7 |
3.6 |
|
|
13 |
9.1 |
6.7 |
5.7 |
5.2 |
4.9 |
4.6 |
4.4 |
4.3 |
4.2 |
4.1 |
3.7 |
3.6 |
3.5 |
3.4 |
|
|
14 |
8.9 |
6.5 |
5.6 |
5.0 |
4.7 |
4.5 |
4.3 |
4.1 |
4.0 |
3.9 |
3.5 |
3.4 |
3.3 |
3.3 |
|
|
15 |
8.7 |
6.4 |
5.4 |
4.9 |
4.6 |
4.3 |
4.1 |
4.0 |
3.9 |
3.8 |
3.4 |
3.3 |
3.2 |
3.1 |
|
|
16 |
8.5 |
6.2 |
5.3 |
4.8 |
4.4 |
4.2 |
4.0 |
3.9 |
3.8 |
3.7 |
3.3 |
3.2 |
3.1 |
3.0 |
|
|
17 |
8.4 |
6.1 |
5.2 |
4.7 |
4.3 |
4.1 |
3.9 |
3.8 |
3.7 |
3.6 |
3.2 |
3.1 |
3.0 |
2.9 |
|
|
18 |
8.3 |
6.0 |
5.1 |
4.6 |
4.2 |
4.0 |
3.8 |
3.7 |
3.6 |
3.5 |
3.1 |
3.0 |
2.9 |
2.8 |
|
|
19 |
8.2 |
5.9 |
5.0 |
4.5 |
4.2 |
3.9 |
3.8 |
3.6 |
3.5 |
3.4 |
3.0 |
2.9 |
2.8 |
2.8 |
|
|
20 |
8.1 |
5.8 |
4.9 |
4.4 |
4.1 |
3.9 |
3.7 |
3.6 |
3.5 |
3.4 |
2.9 |
2.8 |
2.8 |
2.7 |
|
|
21 |
8.0 |
5.8 |
4.9 |
4.4 |
4.0 |
3.8 |
3.6 |
3.5 |
3.4 |
3.3 |
2.9 |
2.8 |
2.7 |
2.6 |
|
|
22 |
7.9 |
5.7 |
4.8 |
4.3 |
4.0 |
3.8 |
3.6 |
3.5 |
3.3 |
3.3 |
2.8 |
2.7 |
2.7 |
2.6 |
|
|
23 |
7.9 |
5.7 |
4.8 |
4.3 |
3.9 |
3.7 |
3.5 |
3.4 |
3.3 |
3.2 |
2.8 |
2.7 |
2.6 |
2.5 |
|
|
24 |
7.8 |
5.6 |
4.7 |
4.2 |
3.9 |
3.7 |
3.5 |
3.4 |
3.3 |
3.2 |
2.7 |
2.6 |
2.6 |
2.5 |
|
|
25 |
7.8 |
5.6 |
4.7 |
4.2 |
3.9 |
3.6 |
3.5 |
3.3 |
3.2 |
3.1 |
2.7 |
2.6 |
2.5 |
2.5 |
|
|
26 |
7.7 |
5.5 |
4.6 |
4.1 |
3.8 |
3.6 |
3.4 |
3.3 |
3.2 |
3.1 |
2.7 |
2.6 |
2.5 |
2.4 |
|
|
27 |
7.7 |
5.5 |
4.6 |
4.1 |
3.8 |
3.6 |
3.4 |
3.3 |
3.1 |
3.1 |
2.6 |
2.5 |
2.5 |
2.4 |
|
|
28 |
7.6 |
5.5 |
4.6 |
4.1 |
3.8 |
3.5 |
3.4 |
3.2 |
3.1 |
3.0 |
2.6 |
2.5 |
2.4 |
2.4 |
|
|
29 |
7.6 |
5.4 |
4.5 |
4.0 |
3.7 |
3.5 |
3.3 |
3.2 |
3.1 |
3.0 |
2.6 |
2.5 |
2.4 |
2.3 |
|
|
30 |
7.6 |
5.4 |
4.5 |
4.0 |
3.7 |
3.5 |
3.3 |
3.2 |
3.1 |
3.0 |
2.5 |
2.5 |
2.4 |
2.3 |
|
|
40 |
7.3 |
5.2 |
4.3 |
3.8 |
3.5 |
3.3 |
3.1 |
3.0 |
2.9 |
2.8 |
2.4 |
2.3 |
2.2 |
2.1 |
|
|
50 |
7.2 |
5.1 |
4.2 |
3.7 |
3.4 |
3.2 |
3.0 |
2.9 |
2.8 |
2.7 |
2.3 |
2.2 |
2.1 |
2.0 |
|
|
60 |
4.0 |
3.2 |
2.8 |
2.5 |
2.4 |
2.3 |
2.2 |
2.1 |
2.0 |
2.0 |
1.7 |
1.7 |
1.6 |
1.6 |
|
|
120 |
3.9 |
3.1 |
2.7 |
2.4 |
2.3 |
2.2 |
2.1 |
2.0 |
2.0 |
1.9 |
1.7 |
1.6 |
1.6 |
1.5 |
|
|
200 |
3.9 |
3.0 |
2.6 |
2.4 |
2.3 |
2.1 |
2.1 |
2.0 |
1.9 |
1.9 |
1.6 |
1.6 |
1.5 |
1.5 |
|
|
500 |
3.9 |
3.0 |
2.6 |
2.4 |
2.2 |
2.1 |
2.0 |
2.0 |
1.9 |
1.8 |
1.6 |
1.5 |
1.5 |
1.4 |
|
|
1000 |
3.9 |
3.0 |
2.6 |
2.4 |
2.2 |
2.1 |
2.0 |
1.9 |
1.9 |
1.8 |
1.6 |
1.5 |
1.5 |
1.4 |
|