Из курса А.А.Авдеева, читавшегося в Страсбургском университете в 2003-2005 годах (перевод на русский и адаптация к традиции русской терминологии еще не закончены)
Analyse bivarié

Нормальное распределение - Z

Adolphe Quételet
Hit Counter
В начало Статистика (введение) Описание одной переменной  Описание двух переменных Библиография
Нормальное распределение t - распределение Стьюдента F распределение Распределение χ2 ¨ Приложения (ANOVA)

[Объяснение]   [Распределение Z]

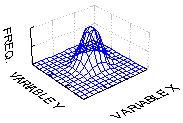
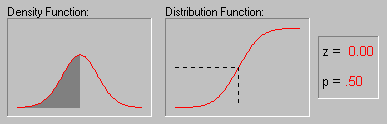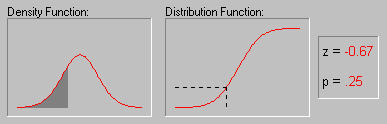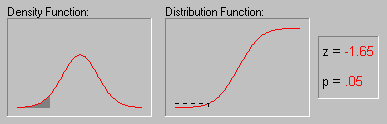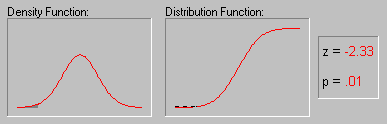Valeurs de la distribution normale standardНормальное распределение, или распределение Гаусса (Gauss) используестя для проверки различных гипотез, включая гипотезу о равенстве двух средних. Это распределение имеет среднюю арифметическую равную 0 и дисперсию равную 1. На графике слева представлена плотность распределения и вероятность (p) соответствующая различным (как говорят "критическим") значениям Z.

Значения в таблице представляют собой площадь, находящуюся под частью кривой, которую описывает стандартизированноя нормальная функция (Gausse)в интервале значений от 0 до  Z. Например, площадь, ограниченная значениями 0 и 2,36, находится  на пересечении линии 2,30 и колонки 0,06. Она равна 0,4909. Если значение Z является отрицательным, то, учитывая симмертичность функции относительно средней, искомая вероятность (площадь) будет находится на пересечении линии и колонки, соответсвующих абсолютному значению Z ( |Z| ). Например, площадь между 0 и -1.3 равна площади между  0 et 1.3; то есть она находится на пересечении линии 1.3 и колоники 0 и равна 0,4032.

Чтобы лучше разобраться в том, как расчитывается вероятность гипотез с помощью таблицы значений нормального распределения, попробуйте самостоятельно построить в Экселе соответствующую таблицу (как ту, что вы видите ниже), используя встроенные функции данного таблятора.

Нормальное распределение

  0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09
0.0 0.0000 0.0040 0.0080 0.0120 0.0160 0.0199 0.0239 0.0279 0.0319 0.0359
0.1 0.0398 0.0438 0.0478 0.0517 0.0557 0.0596 0.0636 0.0675 0.0714 0.0753
0.2 0.0793 0.0832 0.0871 0.0910 0.0948 0.0987 0.1026 0.1064 0.1103 0.1141
0.3 0.1179 0.1217 0.1255 0.1293 0.1331 0.1368 0.1406 0.1443 0.1480 0.1517
0.4 0.1554 0.1591 0.1628 0.1664 0.1700 0.1736 0.1772 0.1808 0.1844 0.1879
0.5 0.1915 0.1950 0.1985 0.2019 0.2054 0.2088 0.2123 0.2157 0.2190 0.2224
0.6 0.2257 0.2291 0.2324 0.2357 0.2389 0.2422 0.2454 0.2486 0.2517 0.2549
0.7 0.2580 0.2611 0.2642 0.2673 0.2704 0.2734 0.2764 0.2794 0.2823 0.2852
0.8 0.2881 0.2910 0.2939 0.2967 0.2995 0.3023 0.3051 0.3078 0.3106 0.3133
0.9 0.3159 0.3186 0.3212 0.3238 0.3264 0.3289 0.3315 0.3340 0.3365 0.3389
1.0 0.3413 0.3438 0.3461 0.3485 0.3508 0.3531 0.3554 0.3577 0.3599 0.3621
1.1 0.3643 0.3665 0.3686 0.3708 0.3729 0.3749 0.3770 0.3790 0.3810 0.3830
1.2 0.3849 0.3869 0.3888 0.3907 0.3925 0.3944 0.3962 0.3980 0.3997 0.4015
1.3 0.4032 0.4049 0.4066 0.4082 0.4099 0.4115 0.4131 0.4147 0.4162 0.4177
1.4 0.4192 0.4207 0.4222 0.4236 0.4251 0.4265 0.4279 0.4292 0.4306 0.4319
1.5 0.4332 0.4345 0.4357 0.4370 0.4382 0.4394 0.4406 0.4418 0.4429 0.4441
1.6 0.4452 0.4463 0.4474 0.4484 0.4495 0.4505 0.4515 0.4525 0.4535 0.4545
1.7 0.4554 0.4564 0.4573 0.4582 0.4591 0.4599 0.4608 0.4616 0.4625 0.4633
1.8 0.4641 0.4649 0.4656 0.4664 0.4671 0.4678 0.4686 0.4693 0.4699 0.4706
1.9 0.4713 0.4719 0.4726 0.4732 0.4738 0.4744 0.4750 0.4756 0.4761 0.4767
2.0 0.4772 0.4778 0.4783 0.4788 0.4793 0.4798 0.4803 0.4808 0.4812 0.4817
2.1 0.4821 0.4826 0.4830 0.4834 0.4838 0.4842 0.4846 0.4850 0.4854 0.4857
2.2 0.4861 0.4864 0.4868 0.4871 0.4875 0.4878 0.4881 0.4884 0.4887 0.4890
2.3 0.4893 0.4896 0.4898 0.4901 0.4904 0.4906 0.4909 0.4911 0.4913 0.4916
2.4 0.4918 0.4920 0.4922 0.4925 0.4927 0.4929 0.4931 0.4932 0.4934 0.4936
2.5 0.4938 0.4940 0.4941 0.4943 0.4945 0.4946 0.4948 0.4949 0.4951 0.4952
2.6 0.4953 0.4955 0.4956 0.4957 0.4959 0.4960 0.4961 0.4962 0.4963 0.4964
2.7 0.4965 0.4966 0.4967 0.4968 0.4969 0.4970 0.4971 0.4972 0.4973 0.4974
2.8 0.4974 0.4975 0.4976 0.4977 0.4977 0.4978 0.4979 0.4979 0.4980 0.4981
2.9 0.4981 0.4982 0.4982 0.4983 0.4984 0.4984 0.4985 0.4985 0.4986 0.4986
3.0 0.4987 0.4987 0.4987 0.4988 0.4988 0.4989 0.4989 0.4989 0.4990 0.4990

Интеграл от  0 до z

Distribution normale